Electron cyclotron maser emission (ECME) represents a major class of meaningful emission mechanism of solar radio bursts. ECME generally occurs in highly allured plasmas with the frequency ratio $omega _ pe/ Omega _ ce < < 1$, caused by energetic electrons with $partial f/ partial v >> 0$, where $f$ represents the velocity distribution function. In solar active areas, this mechanism has been used to millisecond spikes which are identified by high brightness temperature levels, short periods, narrow bandwidths, and strong polarizations.
$, n= 2, 3, …) are more likely to get away. Previous studies utilizing the loss-cone circulation concluded that just essential emissions (i.e., $n= 1$) can grow by means of ECME (e.g., Aschwanden 1990).
To examine the possibilities of harmonic ECME emissions ($ n ge 2$), we conducted totally kinetic electro-magnetic 2D3V particle-in-cell (PIC) simulations, in large domains with a substantial amount of macro-particles to lower the noise level. We utilized horseshoe (Ning et al. 2021a) and loss-cone (Ning et al. 2021b) circulations as the driver of electron cyclotron maser instability (ECMI) to study the wave excitations and the subsequent nonlinear procedures.
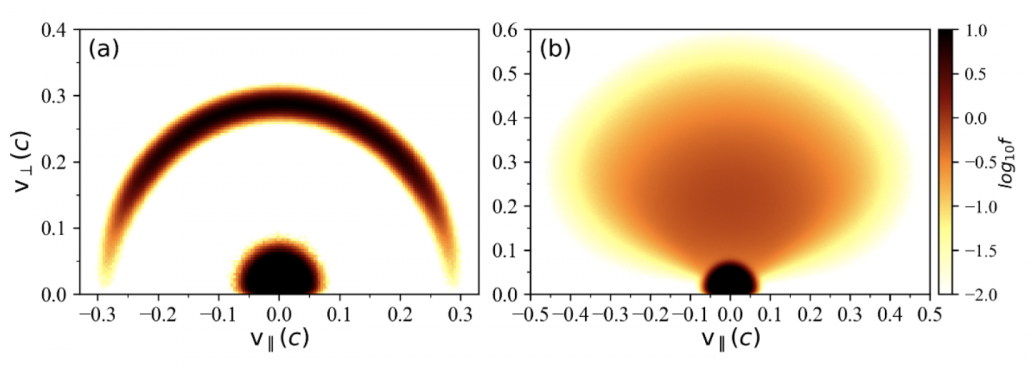
Figure 1. Pictures of the velocity circulation at the start of the simulations with horseshoe (a) and loss-cone (b) circulations. The density ratio of energetic electrons to total electrons are set to be 10%.
Horseshoe circulation
According to in situ measurements, auroral kilometric radiations (AKRs) are released by the horseshoe ECME. As an example of the AKR, solar spikes have actually likewise been connected with energetic electrons of the horseshoe distribution that can form in flare loops with electrons taking a trip toward lower atmosphere (Melrose & & Wheatland 2016).
The horseshoe distribution used to drive the simulation consists of a shell and a double-sided loss-cone distribution (Figure 1( a)). Setting $omega _ / Omega _ = 0.1$, we differed the density ratio of energetic electrons to total electrons ($ n_e/ n_0 $) from 1% to 50%, to imitate the ECME procedure.
Figure 3. Wave dispersion diagrams of electric fields over 7500-8000 $omega _ pe ^ -1 $ along various directions. Panels (a), (b), and (c) show the amplified waves in X1, x2, and z modes. $theta$ represent the angle in between the directions of wavevector and background magnetic field.
Electron cyclotron maser emission (ECME) represents a major class of meaningful emission mechanism of solar radio bursts. Previous studies utilizing the loss-cone distribution concluded that just fundamental emissions (i.e., $n= 1$) can grow through ECME (e.g., Aschwanden 1990).
Pictures of the speed circulation at the start of the simulations with horseshoe (a) and loss-cone (b) circulations. The horseshoe distribution utilized to drive the simulation consists of a shell and a double-sided loss-cone distribution (Figure 1( a)). We employed a double-sided loss-cone circulation (Figure 1( b)).
Figure 4. Optimum wave energies in $vec k $ area over 7000– 8000 $omega _ ^ $; brown and blue represent outcomes in $E_x$ and $E_y$ elements. Possible conditions of wavevectors matching the coalescence condition are overplotted as arrows in the exact same color. Black arrows represent the wavevector of the target mode to be generated. The worths of $theta$ of each wave vector is marked next to.
Figure 3 shows the dispersion diagrams of the magnified waves in the simulation. We discovered that the loss-cone circulation might magnify X1 (panel (a); $omega$ ~ 1.06-1.1 $Omega _ ce $) and Z (panel (b) $omega$ ~ 1.025 $Omega _ ce $) modes by means of ECMI. As a significant result, we acquire strong emissions in X2 along perpendicular and oblique directions at frequencies of 2.05, 2.09, and 2.14 $Omega _ ce $, independently (panel (c)).
We suggest that the X2 emissions are produced by nonlinear coalescence procedures of Z+X 1 and/or Z+Z. This is supported by the following arugments/observations: (1) the matching conditions are well pleased (Figure 4); (2) X2 emissions are magnified at discrete angles and different frequencies; (3) X2 starts to grow behind Z and X1. The energy ratio of X2 to Z mode is ~ 30%, indicating the coalescing procedure is effective in energy conversion
For the very first time, we acquire effective excitations of X2 induced by loss-cone electrons via efficient wave-wave coalescing procedure. Such procedure represents an unique mechanism of X2 emission in plasmas with a low $omega _ pe/ Omega _ $.
Conclusion
We simulated wave excitations by energetic electrons with either horseshoe or loss-cone distribution. We discovered that the horseshoe distribution could produce X2 and X3 at the same time by means of the direct ECME mechanism, while loss-cone distribution could produce X2 through the indirect nonlinear wave-wave coalescence procedure: the loss-cone ECMI magnify X1 and Z modes first, which then coalesce to produce X2 emissions..
The two studies (Ning et al., 2021a, 2021b) shed new lights on the system of harmonic emissions and the resolution of the long-standing getting away issue of ECME. In our simulations, we acquire efficient excitations of X2, with narrow bandwidth and propagation angles, representing high brightness temperatures and strong polarizations of spikes, and describes why just a few percent of the Hard X-ray bursts correlate with spikes.
Based upon the current documents:.
Ning, H., Chen, Y., Ni, S.L., Li, C.Y., Zhang, Z.L., Kong, X.L., & & Yousefzadeh, M., Harmonic electron-cyclotron maser emissions driven by energetic electrons of the horseshoe distribution with application to solar radio spikes, A&A, 2021a, 651, A118, DOI: https://doi.org/10.1051/0004-6361/202140427. Ning, H., Chen, Y., Ni, S.L., Li, C.Y., Zhang, Z.L., Kong, X.L., & & Yousefzadeh, M., Harmonic maser emissions from electrons with the loss-cone circulation in solar active regions, ApJL, 2021b, 920, L40, DOI: https://doi.org/10.3847/2041-8213/ac2cc6.
References.
Aschwanden, M. J. 1990, A&AS, 85, 1141.
Melrose, D. B., & & Dulk, G. A. 1982, ApJ, 259, 844.
Melrose, D. B., & & Wheatland, M. S. 2016, Sol. Phys., 291, 3637.
* Full list of Authors: Hao Ning, Yao Chen, Sulan Ni, Chuanyang Li, Zilong Zhang, Xiangliang Kong, and Mehdi Yousefzadeh.
Figure 2. “Z”, “X2”, “X3”, and “R” stand for the Z mode, second-harmonic X mode, third-harmonic X mode, and the relativistic mode branch.
According to the simulations (Figure 2), the horseshoe distribution can magnify waves in Z and X2 modes (at frequencies of 0.96 and 1.92 $Omega _ ce $) efficiently along the perpendicular direction. The X3 mode likewise grows yet with a lower energy. We note that the amplification of X2 and X3 modes get more efficient with increasing $n _ / n _ 0 $. With $n _ e/ n _ $ varying from 5% to 50%, we approximated the brightness temperature levels of the acquired X2 to be $10 ^ 11 $ K to $10 ^ 15 $ K, consistent with observations of spikes.
Effective amplification of harmonic emissions provides an option to the leaving trouble of the ECME theory. The simultaneous developments of X2 and X3 can explain the multi-harmonic structures observed in solar spikes.
Loss-cone circulation
The loss-cone ECME has actually been extensively investigated by earlier studies, including quasi-linear and direct analyses. The non-linear wave-wave interaction has not been well studied. We performed PIC simulation with a long enough period to study the wave excitations by means of the loss-cone cyclotron resonance instability, and subsequent wave-wave interaction procedures.
We employed a double-sided loss-cone circulation (Figure 1( b)). $ was set to be 10%. $, representing the longest period for simulations ever carried out in studies on the same subject.